Swapping Apples or Oranges
Problem : Requirement is that you are given a list of randomly arranged apples & oranges. You will be given some number of
chances, say N to replace the oranges with apples. Now you have to find the maximum number of continuous
apples you can have after those many number of swaps. To keep the problem straight & bit simple, we can replace
the orange with apple from outside the list. Its anaother version is here.
Solution : Below code is not the optimal one & I feel that it can be improved further but currently putting this solution here.
I have represented apple with 1 & orange with 0.
public class Interview {
public static void main(String[] args) {
int[] fruits = {1,1,1,0,1,0,1,0,0,1,1,1,1,1,0,0,0,0,1,1,1,1,1,1,0};
int swaps = 4;
int maxContOnes = 0;
int k = 0;
int swap = swaps;
int start = 0;
for(int i : fruits) {
if(i == 0) {
if(swap > 0)
swap--;
// There is no chance to swap any zero so move the start counter to next value.
else if(swaps == 0) {
start = k+1;
}
else {
// Set the max count value till the current pointer as all available swaps are consumed now.
if(maxContOnes < k-start) {
maxContOnes = k - start;
}
// if swap = 0 then move the start pointer till one zero is crossed.
while(swap == 0 && start < k) {
if(fruits[start] == 0)
swap++;
start++;
}
// Minus the count of zero by one to count the current zero.
swap--;
}
}
k++;
}
// This is to calculate the value once more if any zero was processed in the last of above iteration.
if(maxContOnes < k-start) {
maxContOnes = k - start;
}
System.out.println(maxContOnes);
}
}
chances, say N to replace the oranges with apples. Now you have to find the maximum number of continuous
apples you can have after those many number of swaps. To keep the problem straight & bit simple, we can replace
the orange with apple from outside the list. Its anaother version is here.
Solution : Below code is not the optimal one & I feel that it can be improved further but currently putting this solution here.
I have represented apple with 1 & orange with 0.
public class Interview {
public static void main(String[] args) {
int[] fruits = {1,1,1,0,1,0,1,0,0,1,1,1,1,1,0,0,0,0,1,1,1,1,1,1,0};
int swaps = 4;
int maxContOnes = 0;
int k = 0;
int swap = swaps;
int start = 0;
for(int i : fruits) {
if(i == 0) {
if(swap > 0)
swap--;
// There is no chance to swap any zero so move the start counter to next value.
else if(swaps == 0) {
start = k+1;
}
else {
// Set the max count value till the current pointer as all available swaps are consumed now.
if(maxContOnes < k-start) {
maxContOnes = k - start;
}
// if swap = 0 then move the start pointer till one zero is crossed.
while(swap == 0 && start < k) {
if(fruits[start] == 0)
swap++;
start++;
}
// Minus the count of zero by one to count the current zero.
swap--;
}
}
k++;
}
// This is to calculate the value once more if any zero was processed in the last of above iteration.
if(maxContOnes < k-start) {
maxContOnes = k - start;
}
System.out.println(maxContOnes);
}
}
One more way to implement for the above problem in a concise way is shown below as contributed by Jatin Agrawal -
public class FindConsecutiveApplesSeqMaxLength {
public static void main(String[] args) {
// System.out.println(getSeqMaxLength(new char[]{'A','A','O','O','A','O','A'}, 3));
// System.out.println(getSeqMaxLength(new char[]{'A','A','O','O','A','O','A'}, 2));
long start = System.nanoTime();
System.out.println(getSeqMaxLength(new char[] {'A','A','A','O','A','O','A','O','O','A','A','A','A','A','O','O','O','O','A','A','A','A','A','A','O'}, 4));
System.out.println(System.nanoTime() - start);
}
private static int getSeqMaxLength(char[] seq, int k) {
int seqMaxLength = 0;
int remaining = k;
int curSeqStart = -1;
int i = 0;
for (; i < seq.length; i++) {
if (seq[i] == 'O') {
if (remaining == 0) {
int curSeqLength = i - 1 - curSeqStart;
if (curSeqLength > seqMaxLength) {
seqMaxLength = curSeqLength;
}
while (seq[++curSeqStart] != 'O');
} else {
remaining--;
}
}
}
int curSeqLength = i - 1 - curSeqStart;
if (curSeqLength > seqMaxLength) {
seqMaxLength = curSeqLength;
}
return seqMaxLength;
}
}
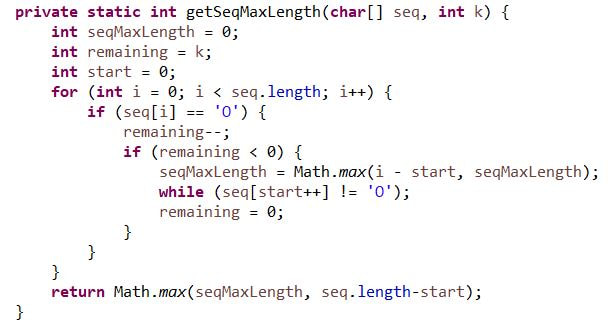
Improved version:
public class FindConsecutiveApplesSeqMaxLength {
public static void main(String[] args) {
// System.out.println(getSeqMaxLength(new char[]{'A','A','O','O','A','O','A'}, 3));
// System.out.println(getSeqMaxLength(new char[]{'A','A','O','O','A','O','A'}, 2));
long start = System.nanoTime();
System.out.println(getSeqMaxLength(new char[] {'A','A','A','O','A','O','A','O','O','A','A','A','A','A','O','O','O','O','A','A','A','A','A','A','O'}, 4));
System.out.println(System.nanoTime() - start);
}
private static int getSeqMaxLength(char[] seq, int k) {
int seqMaxLength = 0;
int remaining = k;
int curSeqStart = -1;
int i = 0;
for (; i < seq.length; i++) {
if (seq[i] == 'O') {
if (remaining == 0) {
int curSeqLength = i - 1 - curSeqStart;
if (curSeqLength > seqMaxLength) {
seqMaxLength = curSeqLength;
}
while (seq[++curSeqStart] != 'O');
} else {
remaining--;
}
}
}
int curSeqLength = i - 1 - curSeqStart;
if (curSeqLength > seqMaxLength) {
seqMaxLength = curSeqLength;
}
return seqMaxLength;
}
}
Improved version: