Below question was asked once in the coding round for Big Product based-
An array of integers 'A' is given and a random integer 'k' is given.
You need to find the list of pairs (a, b) such that below conditions are satisfied-
a. Both a & b should exist in 'A'.
b. a+k = b
c. Both a & b can be same.
d. Pair (a ,b) shouldn't repeat in the result.
e. Result can be a list of arrays or an array of arrays.
Approaches:
1. Brute force: Iterate through the array for each element 'a' to check if a+k is present in the
array. Timem complexity will be O(n^2).
2. Optimal & Simple way: Insert each element element of the array in a Set.
Then iterate through the set for each element 'a' to check if a+k is present in the set. If
present then add array of {a, a+k} in the result list or array.
Time complexity will be O(2n) = O(n)
3. Not so simple & will even increase the complexity: Try with single iteration but it will make
the logic complex. I think, if the given array is sorted then may be we can think about
b-k = a & it wil be faster than (2) else will need to look for a+k = b also & that will make the
logic cumbersome.
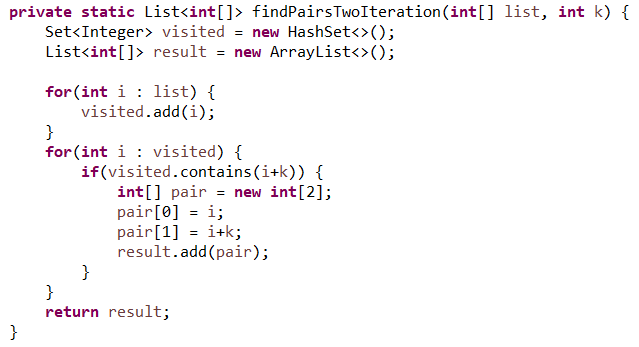
Solution using (2)-
An array of integers 'A' is given and a random integer 'k' is given.
You need to find the list of pairs (a, b) such that below conditions are satisfied-
a. Both a & b should exist in 'A'.
b. a+k = b
c. Both a & b can be same.
d. Pair (a ,b) shouldn't repeat in the result.
e. Result can be a list of arrays or an array of arrays.
Approaches:
1. Brute force: Iterate through the array for each element 'a' to check if a+k is present in the
array. Timem complexity will be O(n^2).
2. Optimal & Simple way: Insert each element element of the array in a Set.
Then iterate through the set for each element 'a' to check if a+k is present in the set. If
present then add array of {a, a+k} in the result list or array.
Time complexity will be O(2n) = O(n)
3. Not so simple & will even increase the complexity: Try with single iteration but it will make
the logic complex. I think, if the given array is sorted then may be we can think about
b-k = a & it wil be faster than (2) else will need to look for a+k = b also & that will make the
logic cumbersome.
Solution using (2)-
Lets try using approach (3).
Implementation is not obvious or intuitive, so not suggesting to use it in general.
It can be 3X faster than (2) above, if the given array is sorted and very large with most
numbers are unique.
But its complexity & testing efforts required may outweigh its benefits.
So giving it here just to show one option using single iteration if given array is sorted-
Implementation is not obvious or intuitive, so not suggesting to use it in general.
It can be 3X faster than (2) above, if the given array is sorted and very large with most
numbers are unique.
But its complexity & testing efforts required may outweigh its benefits.
So giving it here just to show one option using single iteration if given array is sorted-
Just another thought, what if we are not getting the sorted list or sorted array of integers and if try to sort it in our method then it will loose the race to (2) with no arguments.
Though, I still think that if we are getting the sorted array/list then approach (3) will be better than (2), but if it is not sorted. So was just thinking to try with single iteration even if given array/list is not sorted-
Though, I still think that if we are getting the sorted array/list then approach (3) will be better than (2), but if it is not sorted. So was just thinking to try with single iteration even if given array/list is not sorted-


 RSS Feed
RSS Feed
